Congratulations to our group members David Blanik, José Garre-Rubio, and András Molnár who - together with Erez Zohar - have just published their joint paper titled "Internal structure of gauge-invariant projected entangled pair states" in the Journal of Physics A: Mathematical and Theoretical [J. Phys. A: Math. Theor. 58 065301 (2025)]. 

To find out more about their work, take a look at the abstract below and at the open-access article (doi: 10.1088/1751-8121/adae83).

Abstract
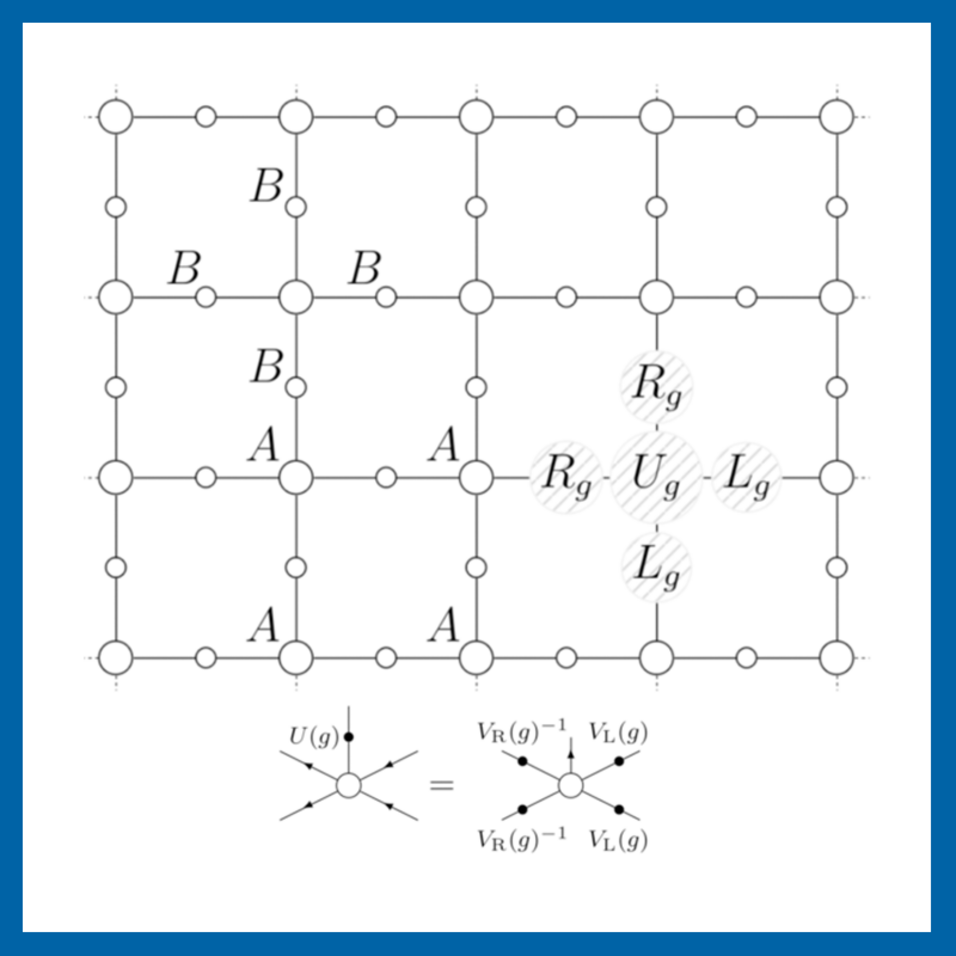
Projected entangled pair states (PEPS) are very useful in the description of strongly correlated systems, partly because they allow encoding symmetries, either global or local (gauge), naturally. In recent years, PEPS with local symmetries have increasingly been used in the study of non-perturbative regimes of lattice gauge theories, most prominently as a way to construct variational ansatz states depending only on a small number of parameters and yet capturing the relevant physical properties. For the case of one-dimensional PEPS (matrix product states - MPS) a bidirectional connection was established between the internal structure of the tensor network, i.e. the mathematical properties of the constituent tensors, and the symmetry. In higher dimensions this has only been done for global symmetries, where in the local (gauge) case it is known only how to construct gauge-invariant states, but not what the symmetry implies on the internal structure of the PEPS. In the present work we complete this missing piece and study the internal structure of PEPS with a gauge symmetry. The PEPS we consider consist of matter and gauge field tensors placed on the vertices and edges, respectively, of arbitrary graphs.

This work has received support through the ERC grant SEQUAM as well as the Austrian Science Fund FWF (grant DOIs 10.55776/P36305 and 10.55776/J4796), and the European Union (NextGenerationEU).