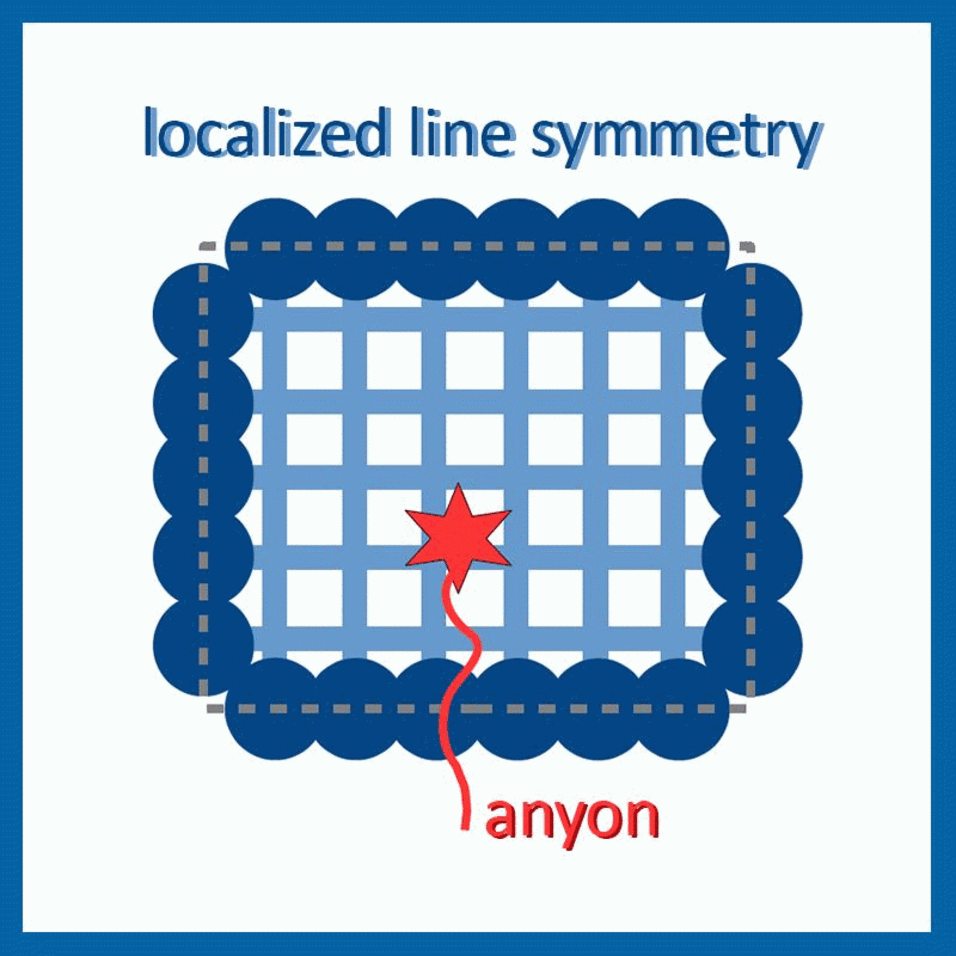
In their recently published paper on "Fractionalization of subsystem symmetries in two dimensions" (Phys. Rev. B 106, 085104), David T. Stephen, Arpit Dua, Dominic J. Williamson, Michael Hermele, and our group member José Garre-Rubio show that a symmetric quantum phase of matter which has so far been deemed nonexistent can in fact be realized in two dimensions. To this end, they combine two scenarios: First, the symmetries that they consider – termed “subsystem symmetries” – do not act on the entire system, but only on part of it, such as on individual lines of the two-dimensional lattice. Second, they consider quantum systems which exhibit so-called “topological order”: Those systems possess global quantum correlations robust against arbitrary local perturbations, and exhibit particle-like excitations with exotic statistics, termed anyons.
In their work, the authors show that in the systems they propose, the subsystem symmetries act in a non-trivial way on the anyons: the symmetry fractionalizes. The important mechanism which allows for this symmetry fractionalization on the anyons is a peculiar restriction of their mobility when the symmetry is enforced, which forces them to move e.g. along lines or fractal strucutres. Specifically, the authors study the different types of subsystem symmetry fractionalization, linear or fractal, in Z2 topologically ordered models. This paper continues the study done on 3D subsystem symmetry fractionalization phases of Phys. Rev. Research 2, 033331 by the same authors.
This work has received support through the ERC grant SEQUAM.