[SEQUAM] Project objectives
Symmetries are at the heart of quantum many-body phenomena in quantum chemistry, condensed matter, and high energy physics. They govern the structure of physical laws, and explain different phases through the mechanism of symmetry breaking. The discovery of novel unconventional phases such as the fractional quantum Hall effect has challenged this view: These phases instead display a global ordering in their entanglement, hindering a characterization in terms of local symmetries.
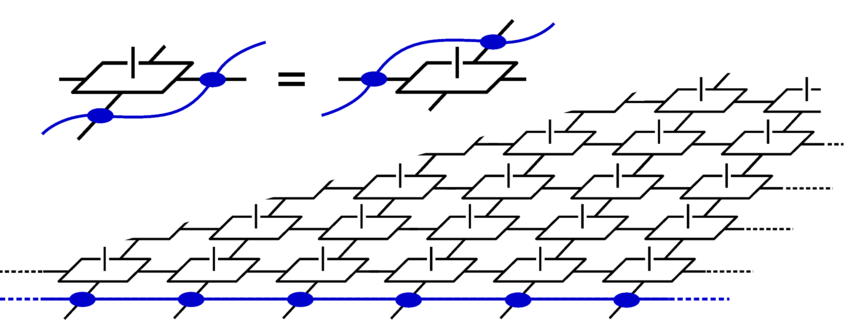
Holography in tensor networks: A bulk entanglement symmetry in the tensor (top left) induces a symmetry at the boundary (the entanglement spectrum) in one dimension less.
The goal of the SEQUAM project is to develop a comprehensive symmetry-centered framework for the study of quantum many-bodysystems across physics, based on the structure of their entanglement. It is placed at the interface between Quantum Information and Quantum Many-Body Physics, and uses the language of Tensor Networks which allows to reconcile locality with global entanglement. Our starting point is the physical symmetry structure of the system of interest. Using Tensor Networks, we move to entanglement space, where we classify the symmetries in the entanglement induced by the physical symmetries, and the way in which the entanglement orders under those symmetries – the entanglement phase. By mapping back to the physical space, we can study the ways in which the entanglement order manifests physically, and obtain a spectrum of powerful analytical, numerical, and experimental probes for unconventional phases. We will apply this framework to a wide range of systems which appear in condensed matter and high energy physics, or are realizable in quantum simulators e.g. with cold gases.
The results of this project will give a unified understanding of unconventional phases, based on physical symmetries and the resulting entanglement order. It will yield their physical manifestations, numerical probes for their detection, and simple ways to realize and probe these models in experimental scenarios, and thus significantly advance our ability to understand, study, and realize complex quantum phases.
