A reliable application of automatic differentiation in tensor network algorithms is the main focus of a new paper titled "Stable and efficient differentiation of tensor network algorithms" which is co-authored by our group members Anna Francuz, Norbert Schuch and Bram Vanhecke. The work has just been published in Physical Review Research [Phys. Rev. Research 7, 013237 (2025)].

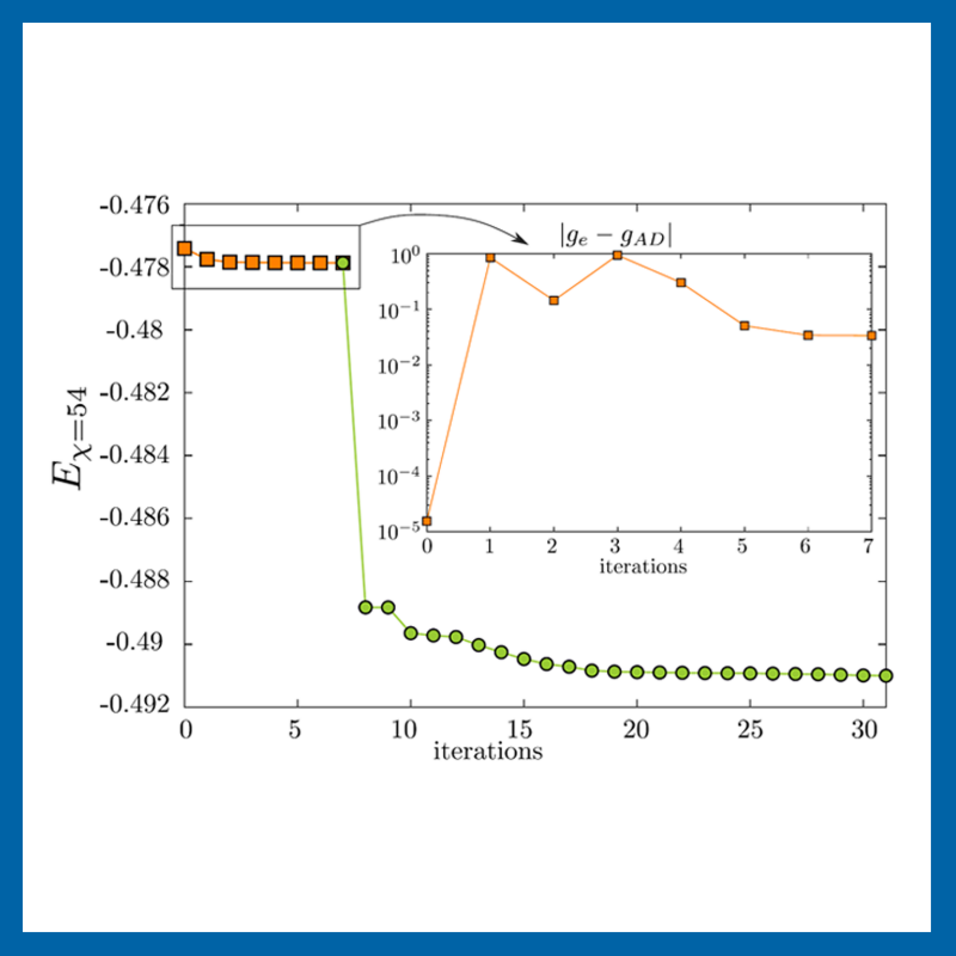
The paper addresses and solves three main issues in the automatic differentiation of tensor network algorithms, which converge to a fixed point and use eigenvalue or singular value decomposition. First, it provides a robust gauge fixing of end result of an iterative procedure for a reliable differentiation of fixed point function. Second, it shows that hitherto used formulas for a gradient of a truncated eigenvalue or singular value decomposition were only approximately correct, and it explicitly provides the correct full expressions, which can be implemented with minimal changes to existing codes. Finally, it uses an gauge freedom inherent to tensor networks to eliminate divergences which appear in the gradient due to the degenerate spectrum of the corner matrix in the Corner Transfer Matrix algorithm. Finally it shows that implementing the aforementioned improvements leads to an optimization algorithm reaching global minimum faster without getting stuck due to incorrect descent direction.

To find out more, please take a look at the open-access article on the Physcial Review Research website.

This work has received support through the ERC grant SEQUAM as well as the Austrian Science Fund FWF (grant DOIs 10.55776/ESP306, 10.55776/COE1, 10.55776/P36305 and 10.55776/F71), and the European Union (NextGenerationEU). Numerical calculations were performed using the Vienna Scientific Cluster (VSC).