This question, stimulated by the recent discovery of higher-order topological insulators, has now been answered by Anna Hackenbroich, Ana Hudomal, B. Andrei Bernevig, Nicolas Regnault, and our research group leader Norbert Schuch. Their paper titled "Fractional chiral hinge insulator" has just been featured as an "Editors' Suggestion" in Physical Review B.
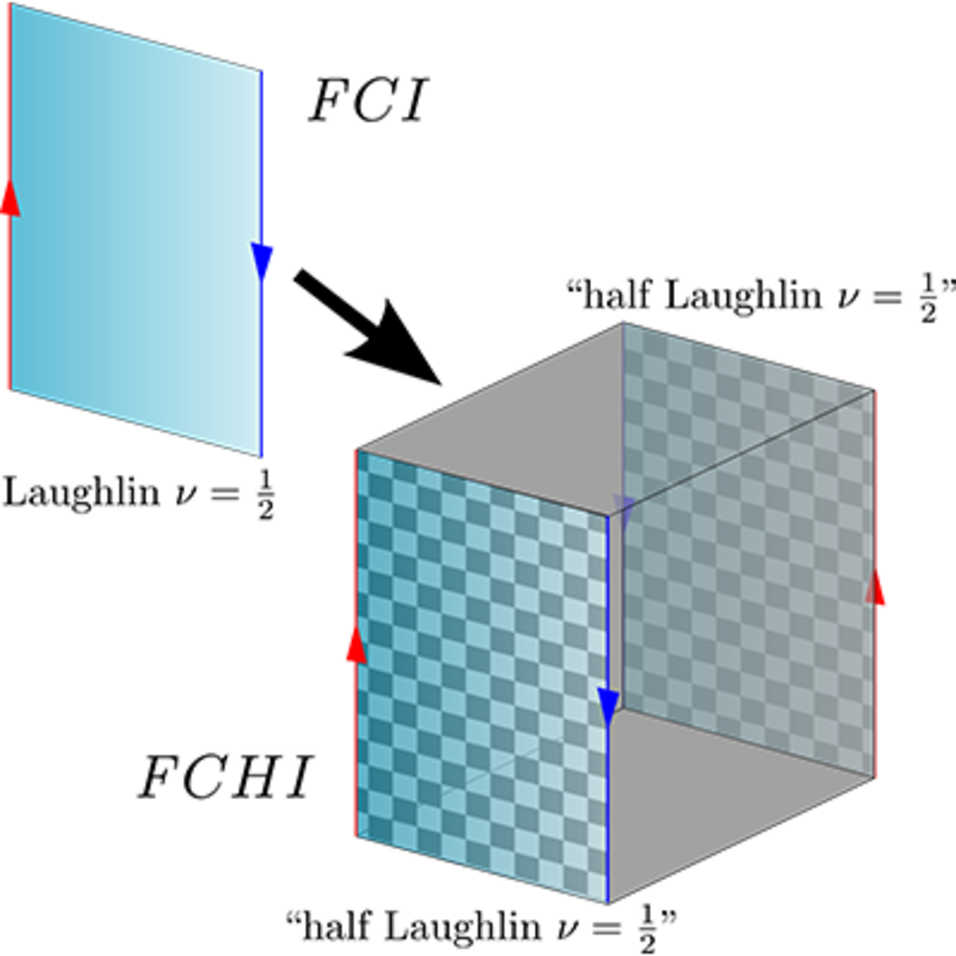
In their work, the authors investigate the interplay of higher-order topological insulators and strong interactions by using a model wavefunction, which they study using large-scale Monte Carlo simulations. They show that this interplay gives rise to fractionalized chiral hinge modes, similar to the physics of the Laughlin state. These results indicate that the gapped surfaces of the model exhibit novel physics which clearly departs from any behavior known for conventional two-dimensional topological order, suggestive of "half a Laughlin state" at each surface.
The paper can be found on the journal's website, as well as on the arXiv.
This work has received support through the ERC grant SEQUAM.