Robust preparation of quantum states in isolated, interacting quantum systems remains a significant challenge. Various experimental platforms can realize unitary quantum dynamics generated by a Hamiltonian with a few controllable parameters. However, our understanding of how to prepare entangled states via such continuous unitary dynamics remains limited.
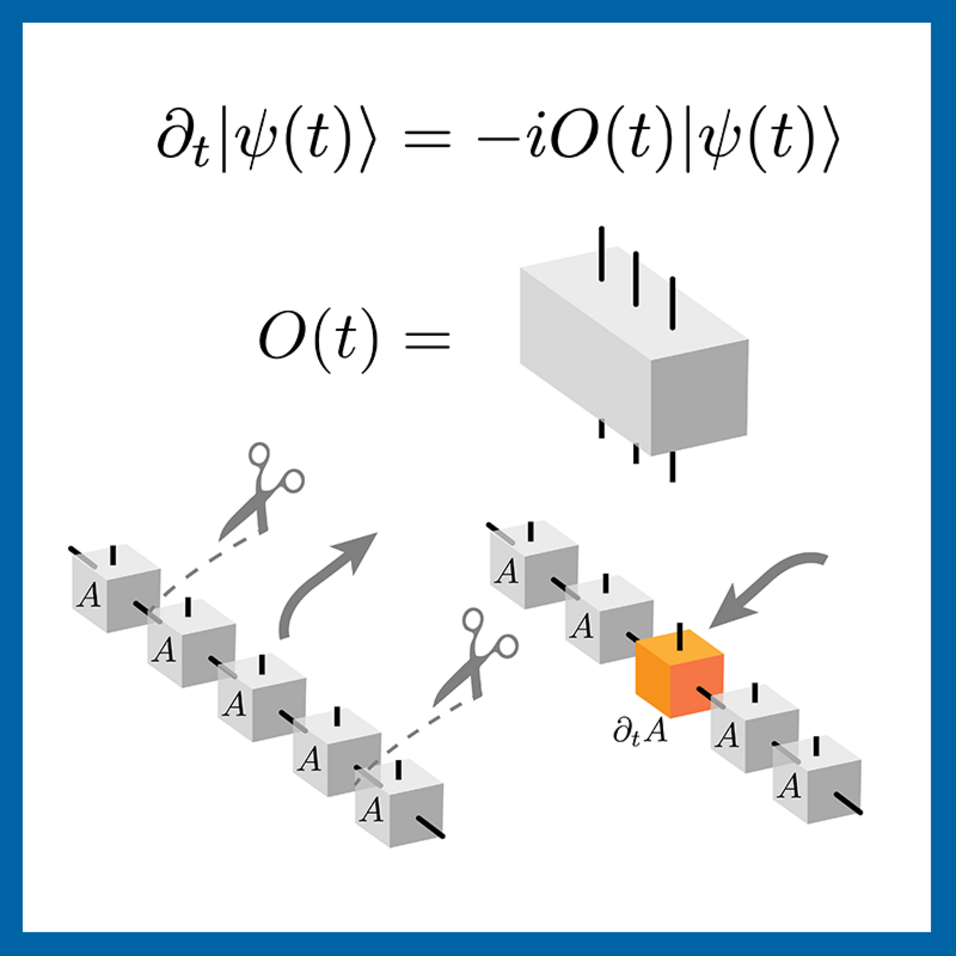
In their work titled "Tangent Space Generators of Matrix Product States and Exact Floquet Quantum Scars" [PRX Quantum 5, 040311 (2024)], Marko Ljubotina, Elena Petrova, Norbert Schuch, and Maksym Serbyn propose a constructive approach for preparing one-dimensional entangled states representable as matrix product states. Matrix product states are known to efficiently represent ground states of gapped systems as well as short-term nonequilibrium dynamics.
The authors split the full evolution problem into infinitesimal steps and construct generators of dynamics along a desired tangent space direction in the manifold of MPS. They construct an explicit sequence of Hermitian operators – i.e., Hamiltonians generating time dynamics – which realize an evolution along the desired tangent space direction, and demonstrate that the resulting operators can be made quasilocal, with longer-range operators having exponentially suppressed weight.
Applying the approach to a periodic trajectory representable as matrix product states results in a time-periodic quasi-local Hamiltonian. The authors show that the unitary operator that generates dynamics over one period of the trajectory (Floquet operator) features a non-thermal eigenstate with low entanglement, in contrast to the common expectations that the entire spectrum of the Floquet operator obeys the eigenstate thermalization hypothesis (ETH). This non-thermal eigenstate can be interpreted as a Floquet quantum many-body scar. Their work provides a route for creating matrix product states via unitary dynamics and, at the same time, allows to construct Floquet models with quantum many-body scars.
For more information on this work take a look at the open-access paper at PRX Quantum or on arXiv.
This work has received support through the ERC grant SEQUAM and the Austrian Science Fund FWF (grant DOIs 10.55776/COE1, 10.55776/P36305 and 10.55776/F71), and the European Union (NextGenerationEU).